Using mitochondrial haplotypes
mtDNA.RmdWhy use mitochondrial data
Using data on the sharing of mitochondrial (mt) haplotypes makes it possible to distinguish between maternal/matrilineal and paternal/patrilineal relatives. For example, half-siblings sharing the same mother will always have the same mitochondrial haplotype, while half-siblings sharing the same father may have different haplotypes. Similarly, an individual always has the same mitochondrial haplotype as its maternal grandmother, but not (necessarily) as its paternal grandmother.
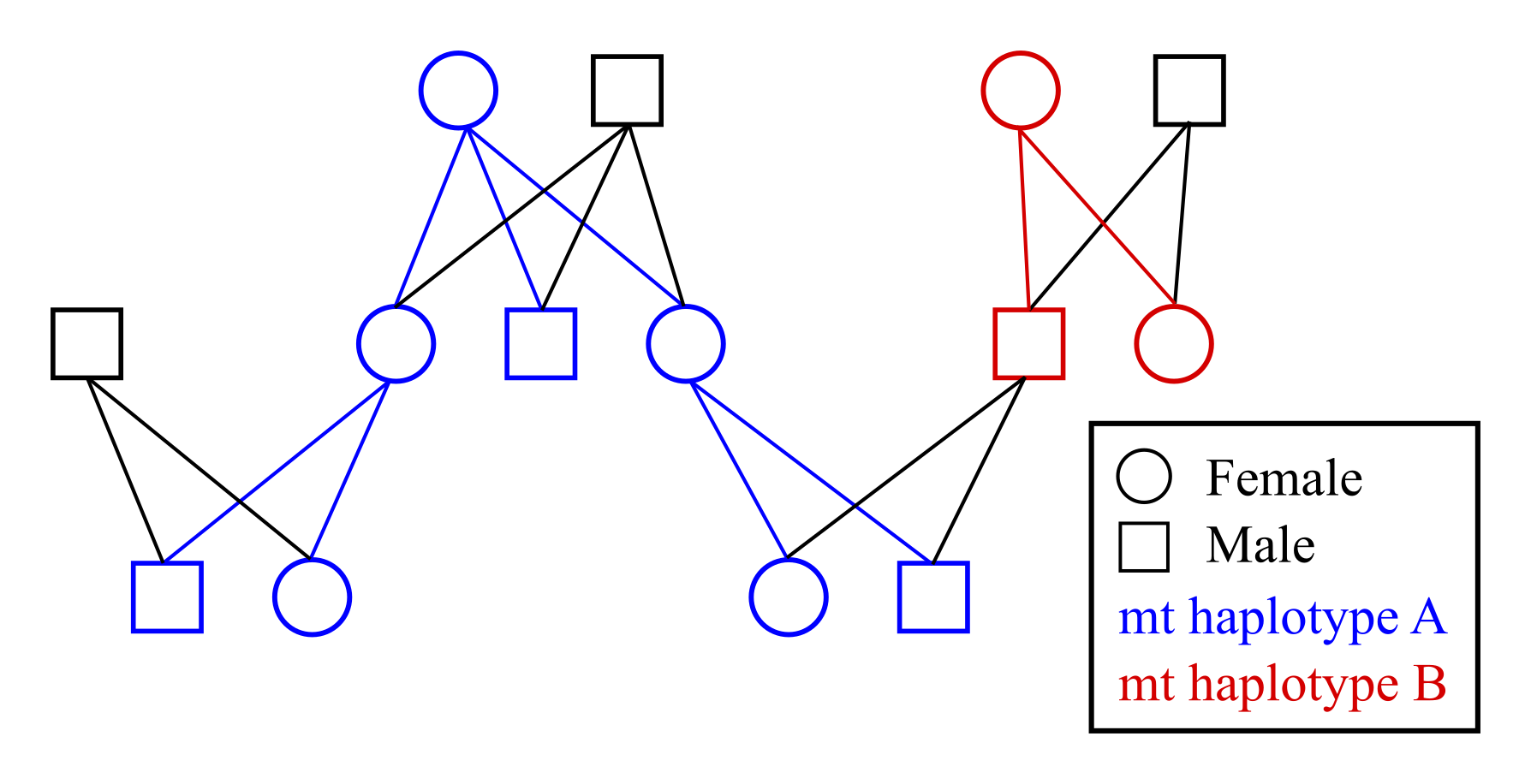
Example pedigree with colour coded mitochondrial haplotype inheritance
Limitations
- Some paternal relatives may share the same mitochondrial haplotype, especially in small populations or if the population was founded by a limited number of females;
- Mitochondrial haplotype sharing does not help distinguish between maternal half-siblings, full avuncular, and grand-parental pairs, and so when generations overlap the assignment rate may still be below 100%;
- It can be challenging to set a threshold between ‘same’ versus
‘different’ haplotypes, especially with a non-negligible genotyping
error rate, limited number of polymorphic mitochondrial markers, and/or
low call rate. The most conservative approach as input for
sequoiais to set any uncertain pairs to ‘same’ (see next section).
Input
From package version 2.7 onwards, function sequoia() has
the input parameter mtSame. This is a matrix with for each
pair of individuals indicating whether they share the same mitochondrial
haplotype (1) or have different haplotypes (0).
The algorithm focusses on the differences: if two individuals
and
are close relatives according to the autosomal SNPs, and have different
mitochondrial haplotypes (mtsame[i,j]==0), they cannot be
maternal/matrilineal relatives, and thus must be paternal/patrilineal
relatives. In contrast, if two individuals share the same mitochondrial
haplotype (mtsame[i,j]==1), they may be maternal relatives,
but it cannot be excluded that they are paternal relatives.
Therefore, if it is unclear or unknown whether two individuals share
the same mitochondrial haplotype, this should be coded as 1
or NA, which is interpreted as ‘may or may not be the
same’, while 0 is interpreted as ‘definitely different’ (=
definitely not maternal relatives).
| maternal | paternal | unrelated | ||
|---|---|---|---|---|
| same | OK | OK | OK | |
| mt haplotype | different | X | OK | OK |
| ? | OK | OK | OK |
Example
This example uses a single cohort from pedigree
Ped_HSg5, which is included in the package. Both females
and males have multiple mates, resulting in both maternal and paternal
half-siblings as well as full siblings. We pretend here that none of the
parents are genotyped, and that each breeding female has a unique
mitochondrial haplotype.
First, let us create a dataset for this example:
library(sequoia)
# pedigree subset
id_subset <- as.character( LH_HSg5[LH_HSg5$BirthYear == 2001, 'ID'] )
Ped_sub <- Ped_HSg5[Ped_HSg5$id %in% id_subset,]
# assign a mitochondrial haplotype code to each founding female
founder_females <- as.character( LH_HSg5[LH_HSg5$BirthYear == 2000 & LH_HSg5$Sex==1, 'ID'] )
mtHaps_founders <- setNames( LETTERS[1:length(founder_females)], founder_females)
head(mtHaps_founders)## a00001 a00002 a00003 a00004 a00005 a00006
## "A" "B" "C" "D" "E" "F"
# infer mitochondrial haplotypes for all matrilineal descendants of individuals
# with known haplotypes
source('https://raw.githubusercontent.com/JiscaH/sequoiaExtra/main/infer_mt_haplo.R')
mtHaps_all <- infer_mt_haplotype(Ped_sub, mtHaps_founders)
mtHaps_all[41:50]## a01036 a01039 a01042 a01043 a01046 a01047 a01048 a01050 a01051 a01053
## "F" "D" "R" "R" "F" "F" "F" "E" "E" "H"
# add mitochondrial haplotype code to pedigree
Ped_sub$mt <- mtHaps_all[as.character(Ped_sub$id)]
head(Ped_sub)## id dam sire mt
## 41 a01001 a00014 b00011 N
## 42 a01002 a00014 b00011 N
## 43 b01003 a00014 b00011 N
## 44 b01004 a00014 b00011 N
## 45 a01005 a00013 b00001 M
## 46 b01006 a00013 b00001 MThe function infer_mt_haplotype() is not included in the
package, but available from . It can also be used on real
data, when mother-offspring relationships are reliably known, e.g. from
behavioural observations, and only a subset of individuals is genotyped
for mitochondrial markers. It infers haplotypes for both ancestors and
descendants of individuals with known haplotypes, and then iterates a
few times to infer haplotypes for all matrilineal relatives.
Then, create the matrix with for each pair of individuals whether they have the same (1) or different (0) haplotype:
mt_same <- outer(mtHaps_all, mtHaps_all, FUN = function(x,y) as.numeric(x==y))
mt_same[41:48, 41:48]## a01036 a01039 a01042 a01043 a01046 a01047 a01048 a01050
## a01036 1 0 0 0 1 1 1 0
## a01039 0 1 0 0 0 0 0 0
## a01042 0 0 1 1 0 0 0 0
## a01043 0 0 1 1 0 0 0 0
## a01046 1 0 0 0 1 1 1 0
## a01047 1 0 0 0 1 1 1 0
## a01048 1 0 0 0 1 1 1 0
## a01050 0 0 0 0 0 0 0 1Simulate autosomal SNP data, with none of the parents genotyped:
Geno_A <- SimGeno(Ped_sub, nSnp=500, ParMis=1, SnpError=1e-3)Run sequoia with & without mtSame (note that these
can take a couple minutes to run):
SeqOUT_regular <- sequoia(Geno_A, LH_HSg5, quiet=TRUE)
SeqOUT_mt <- sequoia(Geno_A, LH_HSg5, mtSame = mt_same, quiet=TRUE)Count number of half-siblings assigned in each run:
##
## FS M O P S U
## 634 191 382 191 284 78974##
## FS M MHS O P PHS S U
## 640 192 704 384 192 1472 232 50008Thus, without mtSame not a single half-sibling
relationship is assigned, as it cannot be determined whether they are
maternal or paternal half-siblings. In contrast, with
mtSame hundreds of half-siblings are assigned.
In this example, the effect of mtSame on the number of
individuals to which a dummy parent is assigned is negligible, as every
individual has several full-siblings, and a dummy mother and father are
assigned to each full-sibling cluster. Some additional full siblings are
assigned: with default option Complex = 'full' the
distinction between full siblings versus e.g. ‘half siblings as well as
cousins’ (r=3/8) is not always clear, and the assignment of additional
maternal and/or paternal half-siblings may clarify the full sibling
relationships.
For a graphical representation of these results you can run:
PlotRelPairs(RelM_regular)
PlotRelPairs(RelM_mt)